|
|
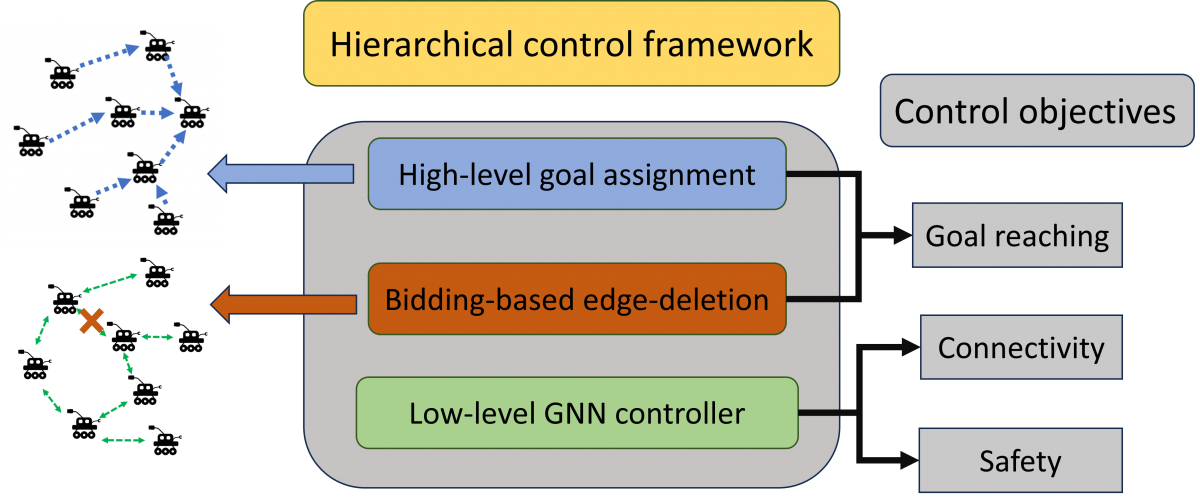
Hierarchical Control Framework for MAS controlThe main focus of this work is design of scalable algorithms for safe multi-agent coordination and control, with deadlock resolution in mind. The proposed approach consists of a high-level planner that helps resolve deadlocks while a low-level controller that helps maintain connectivity and safety. The low-level controller is based on our recent results in CoRL'23 paper where we proposed a Graph Neural Network (GNN)-based control design mechanism for distributed and scalable safe control of large-scale multi-agent systems (MAS). Some preliminary experimental results are documented here in this video and are submitted to ICRA'24.
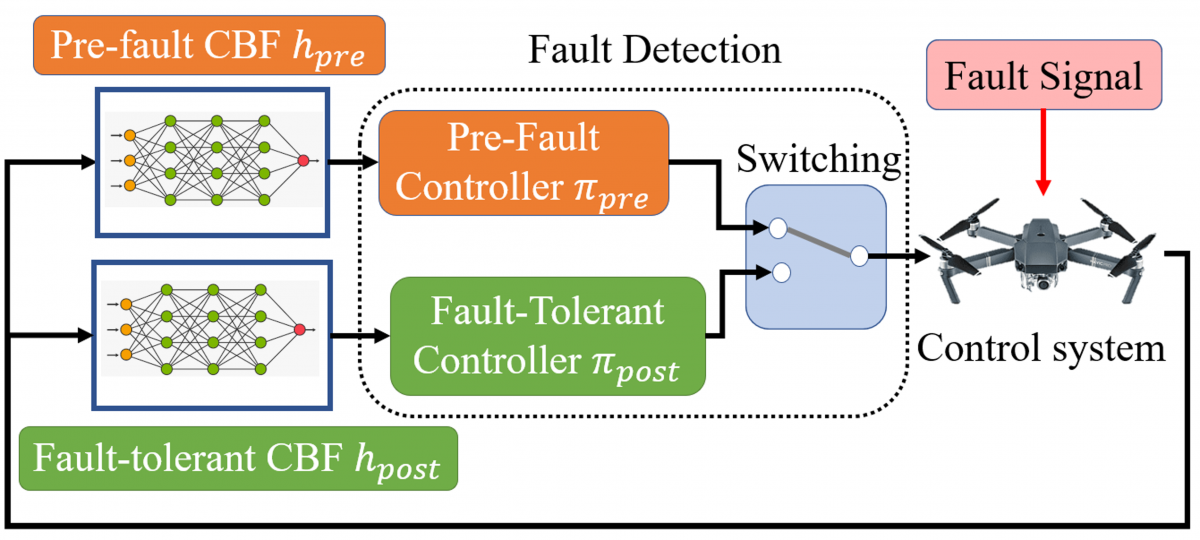
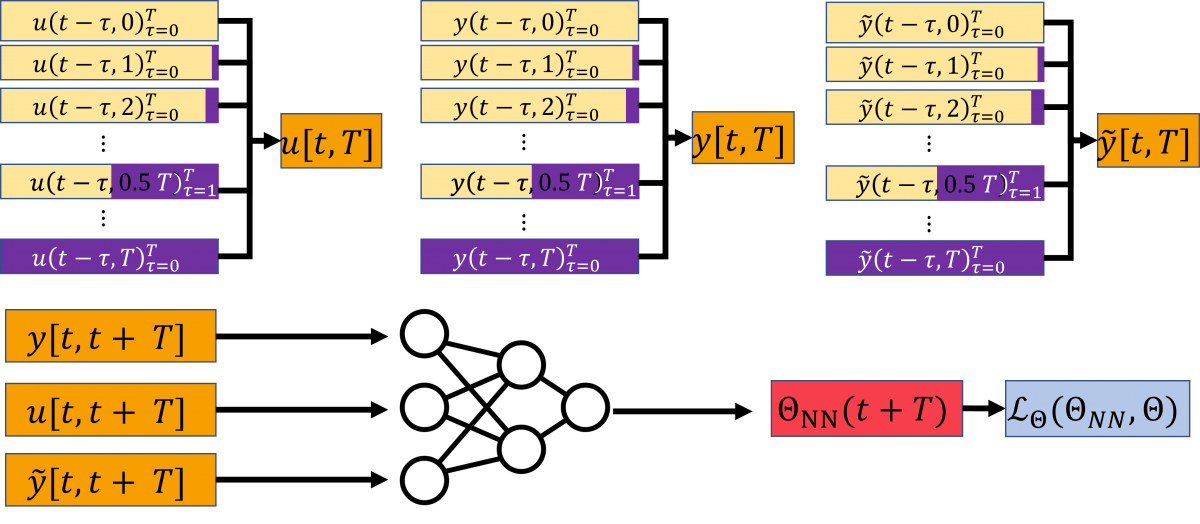
Neural Model-free Fault Detection and IdentificationThe goal of this research project is to develop model-free fault-detection and identification mechanism that can predict faults and failures in system actuators with high accuracy. We use LSTM-based neural network architecture, and a model-free approach where only the system output and the commanded input are used for predicting faults in actuators and monitoring their health. (References Allerton'23, LCSS'23).
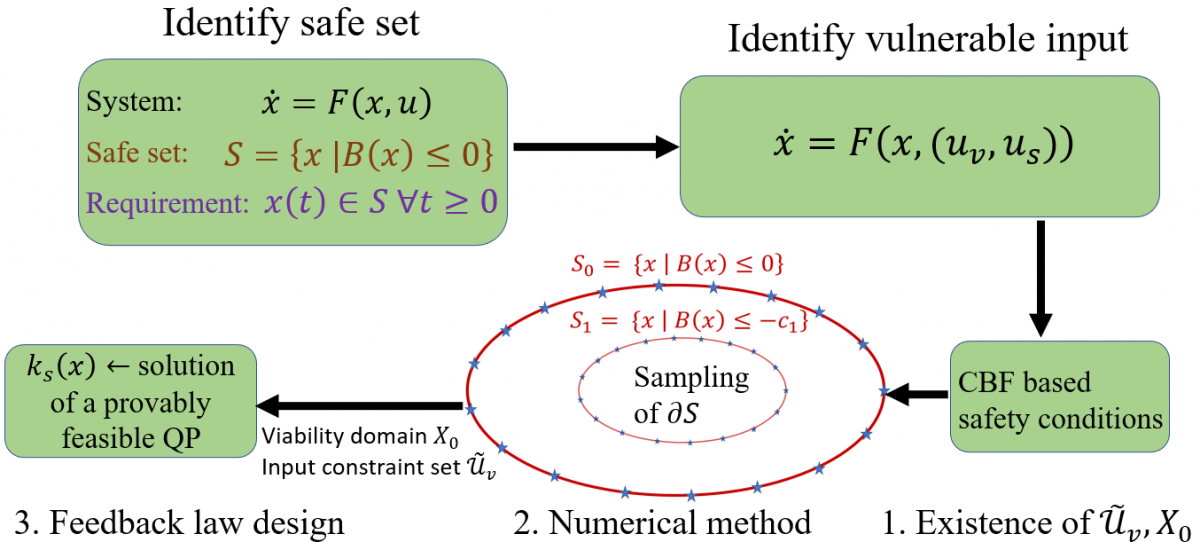
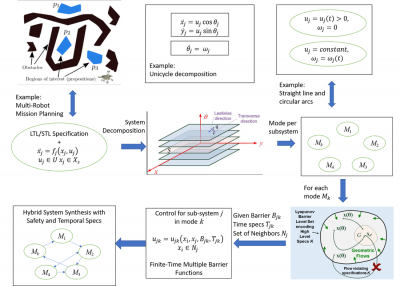
Secure and Resilient Design of Internet of Battlefield ThingsThe goal of this research project is to have networks of autonomous and non-autonomous systems consisting of drones, robots, sensors, and biometric wearable devices communicating and sharing information perform their operation safely while being subject to cyber attacks. Key results include Computationally effective method of computing a viability domain for provable safety for a system under attack and CBF-based effective attack detection mechanism for attack recovery. (References SnP '23, CCTA'22, CDC'22, ACC'23): From High-Level Task Specifications to Low-Level Geometric Control via Lyapunov AbstractionsThe goal of this research project is to narrow the existing gap between high-level discrete task planning and low-level continuous control in complex multi-agent missions within a control-theoretic framework. The main idea lies on the pairing of a Lyapunov-like barrier function and a geometric flow using notions and tools from geometric control and dynamical systems theory. The proposed method offers a reactive motion planning, decision-making and control design mechanism that is scalable with the number of agents and tasks, and thus applicable to large-scale systems involving hundreds of agents. (References: Frontiers '21, Automatica '22, LCSS'22).
Robust Multi-agent controlVector-field based control design:
We worked on designing safe and robust path planning algorithms for multi-agent systems. The vehicles considered can be multi-rotors or fixed-wing UAVs. We devised robust path planning algorithms for multi-agent deconfliction in the presence of sensor uncertainties, wind disturbances and measurement errors, and computed safe controllers in a distributed manner. (References: AIAA GNC'19, AIAA JGCD '19).
Quadratic program based control design:
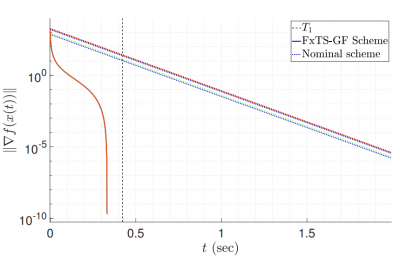
Then, we explored Quadratic Program (QP) based method for a systematic way of control synthesis for multi-objective problems involving spatio-temporal constraints (see CDC' 19 paper). We proposed a new class of Control Lyapunov Functions (CLFs) termed as Fixed time-CLFs along with Control Barrier Functions to guarantee convergence of the closed-loop trajectories to a goal set, within a fixed time, while maintaining safety with respect to unsafe set(s). Our more recent results include robustness analysis of FxT-CLFs (CDC '20 paper, ACC '21 paper) and non-smooth analysis for optimization based control design (CDC '20 paper). Fixed-time Stable optimization schemesWe explored the theory of Fixed-time stability to design modified fixed-time gradient flows (FxTS-GF) for solving constrained and unconstrained optimization, and min-max problems within a fixed time (see our TAC '20, AAAI'22 paper). We extended the idea to a general Distributed Optimization framework in this paper, and to the specific problem of Distributed Economic Dispatch in this paper. Our results can also be used for Sparse-recovery within fixed time as shown in this paper.
|